카이제곱 검정(Chi-Square Test)은 범주형 데이터의 분포를 분석할 때 사용하는 통계적 방법입니다. 주로 관찰된 데이터가 기대되는 분포와 얼마나 일치하는지를 검정하거나, 두 개 이상의 범주형 변수 간의 독립성을 검정하는 데 사용됩니다. 카이제곱 검정에는 여러 종류가 있지만, 여기서는 주로 사용되는 두 가지를 설명하겠습니다: 카이제곱 적합도 검정과 카이제곱 독립성 검정.
1. 카이제곱 적합도 검정 (Chi-Square Goodness of Fit Test)
카이제곱 적합도 검정은 관찰된 데이터가 특정한 이론적 분포에 얼마나 잘 맞는지를 검정합니다. 예를 들어, 주사위를 던졌을 때 모든 면이 동일한 확률로 나오는지 확인할 수 있습니다.
과정:
- 가설 설정:
- 귀무가설(H0): 관찰된 데이터는 기대되는 분포와 일치한다.
- 대립가설(H1): 관찰된 데이터는 기대되는 분포와 일치하지 않는다.
- 기대도수 계산: 각 범주에 대한 기대도수(expected frequency)를 계산합니다.
- 카이제곱 통계량 계산: 카이제곱 통계량은 다음과 같이 계산됩니다:
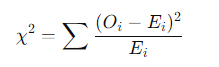
여기서 Oi는 관찰도수(observed frequency), Ei는 기대도수(expected frequency)입니다.
4.자유도 결정: 자유도(df)는 범주의 수(n)에서 1을 뺀 값입니다. 즉, df=n−1
5. p-값 계산 및 결론 도출: 카이제곱 분포표를 사용하여 p-값을 계산하고, 이를 통해 귀무가설을 기각할지 여부를 결정합니다.
2. 카이제곱 독립성 검정 (Chi-Square Test of Independence)
카이제곱 독립성 검정은 두 개의 범주형 변수 간의 독립성을 검정합니다. 예를 들어, 성별과 선호하는 제품 유형 간에 연관성이 있는지 확인할 수 있습니다.
과정:
- 가설 설정:
- 귀무가설(H0): 두 변수는 독립이다.
- 대립가설(H1): 두 변수는 독립이 아니다.
- 교차표 생성: 두 변수의 교차표(contingency table)를 생성합니다.
- 기대도수 계산: 각 셀에 대한 기대도수를 계산합니다:

4.카이제곱 통계량 계산: 앞서 언급한 카이제곱 통계량 공식으로 계산합니다.
5.자유도 결정: 자유도는 (행의수−1)×(열의수−1)입니다.
6.검정 통계량(chi-square statistic) 값 계산 및 결론 도출: 카이제곱 분포표를 사용하여 검정 통계량(chi-square statistic) 값을 계산하고, 이를 통해 귀무가설을 기각할지 여부를 결정합니다.
요약
카이제곱 적합도 검정:
- 한 개의 범주형 변수의 분포가 기대되는 분포와 일치하는지를 검정합니다
- 관찰된 데이터가 기대되는 분포와 일치하는지를 검정합니다.
- 주사위를 던져서 나오는 눈의 분포가 균일한지 확인할 때 사용할 수 있습니다.
카이제곱 독립성 검정:
- 두 개의 범주형 변수 간의 독립성을 검정합니다
- 두 개의 범주형 변수 간의 독립성을 검정합니다.
- 성별과 선호 제품 유형 간의 관계가 있는지를 확인할 때 사용할 수 있습니다.
'통계' 카테고리의 다른 글
| 가설검정, 통계적 유의성, t검정 (0) | 2024.05.29 |
|---|---|
| 표본분포, 신뢰구간, 정규분포 (0) | 2024.05.29 |
| ANOVA에 대한 간략정리 (1) | 2024.05.29 |
